The other day I stumbled across Huffman coding and Huffman trees accidentally, I had learned about them within my CS curriculum but never really gave them a second thought. But turns out they're super super cool and interesting. So I implemented it on my own and compressed down Herman Melville's Moby Dick.
Ideally Text compression unlike image or video needs to be lossless because we cannot afford to miss characters as that might change intended meaning of the words or simply just not make any sense.
I really don't want to get into the history of how this came to be, so I'll just define what Huffman coding is, what we do to achieve it and show you my implementation.
Huffman Coding
To keep things simple, we usually represent all characters we use in the English language with 8 bit ASCII codes where each character is mapped to a unique character sequence. On the other hand with Huffman coding we can assign shorter binary sequences to characters according to their frequency. We assign shorter codes to more frequently occurring characters and longer ones to less frequent characters, some characters may have a mapping longer than 8 bits, but it on average tends to balance out due to the more frequently occurring characters being assigned shorter codes.
Huffman Tree
We build a tree structure, often called a Huffman tree to encode and decode our binary mapping for every character. Each leaf node represents a character, and each interior node contains the sum of the frequency of its children. Once our tree is ready we can traverse it to encode and decode. When we pick the left subtree we add a 0 to your character mapping, 1 otherwise. We can use this to formulate a unique binary mapping to a character.
How to build a Huffman tree
Step by step we follow these steps.
- Count frequencies
- Create leaf nodes corresponding to each character
- Build a min heap with each item as node ordered by frequency
- To build the actual tree
- Remove two nodes with lowest frequencies
- Create a new node with the sum of frequencies as the parent, left child as smaller node and right child as the larger node
- push new node back into heap
- Repeat till there is a complete tree with all characters included in the tree.
Process and Pseudo Code Snippets
To keep the process simple, the conversions to binary were stored in text files, the original book in binary came out to be 9720 kB.
1. Character Frequency Count
We read all the characters in the source file and then count how many times each one occurs and create a frequency map for all characters.
This is so we can determine at what depth of the Huffman tree does a character go.
It was done as simply as
def char_freq():
file = read('moby-dick.txt')
freqs = {}
for c in file:
key = "<SPACE>" if c == " " else ("\\n" if c == "\n" else c)
freqs[key] = freqs.get(key, 0) + 1
return freqs
2. Define a Node structure to hold a character
We define a node data structure that can hold values like character, label, frequency, left sub-tree and right sub-tree, we also overload the function of the < character.
The code looks like following
class Node:
def __init__(self, char, freq, left, right):
self.char = char
self.freq = freq
self.left = left
self.right = right
def __lt__(self, other):
return self.freq < other.freqthe __lt__ helps the heap we will use to implicitly handle how we determine which node is larger
3. Building the Huffman Tree
We build a heap with all characters as their individual nodes, we take two of the smallest nodes create a parent node out of the sum of frequencies of those nodes, the left child is the smaller node and right child is the larger node, we then push it back into the heap. we repeat this process till there is only one node (i.e. a tree containing all the character nodes) left in the heap.
The process looks something like
import heapq
def build_huffman_tree():
heap = [Node(c, f) for c, f in freqs.items()]
heapq.heapify(heap)
while len(heap) > 1:
left = heap.heappop()
right = heap.heappop()
merged = Node("Internal", left.freq + right.freq, left, right)
heap.push(merged)
root = heap[0]
return root The tree will look like this when represented using graphviz
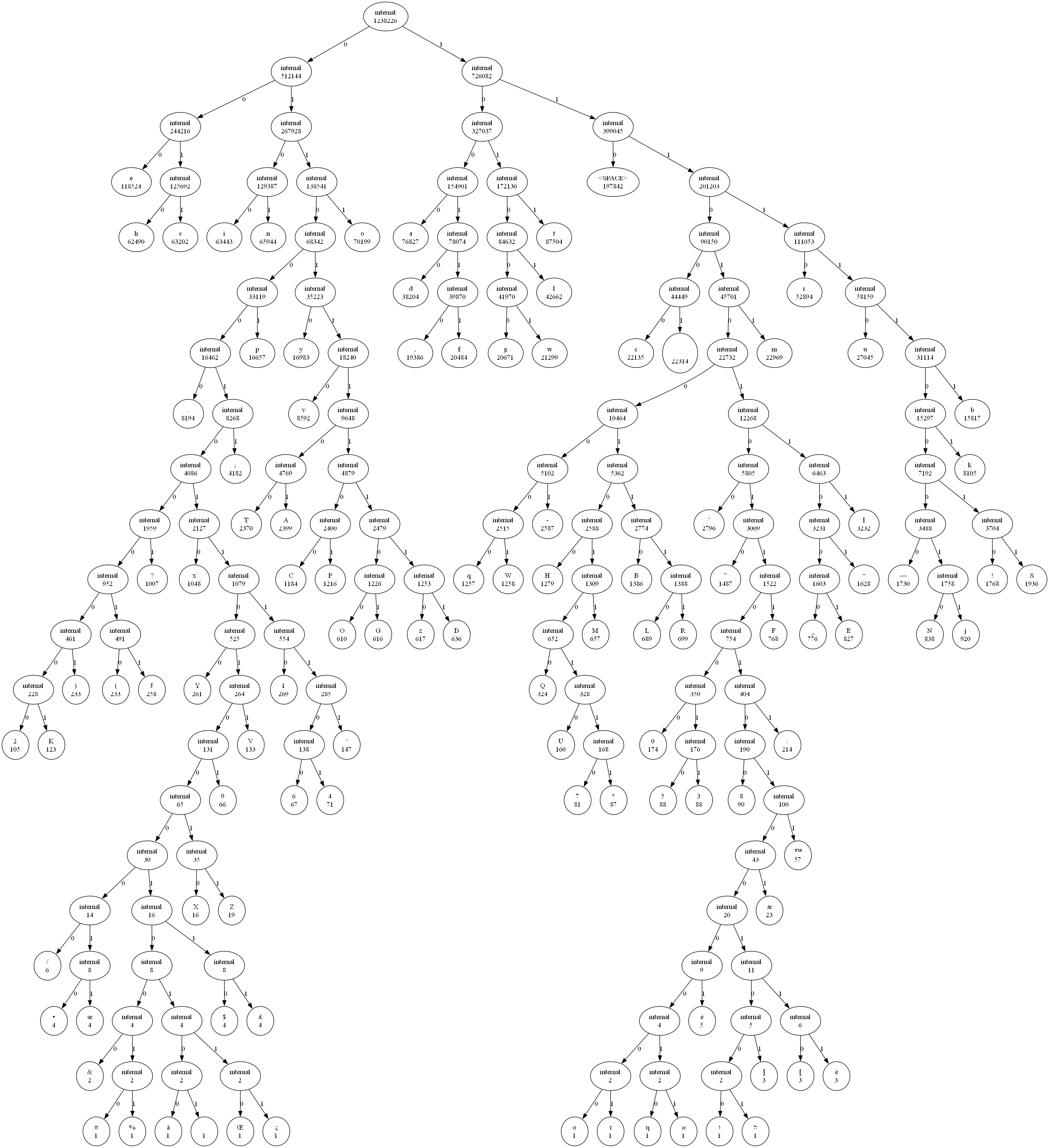
4. Generate Huffman Code mappings for all Characters
We perform a Root to Leaf traversal of each unique path on the tree and generate a unique Huffman code mapping for each of the characters in the piece of text by adding a 0 to the code if we traverse left, and adding a 1 if we traverse right.
The code would look like the following.
def generate_huffman_codes(root, prefix="", code_map={}):
if root is not None:
if root.char != "Internal":
code_map[root.char] = prefix
generate_huffman_codes(root.left, prefix + "0", code_map)
generate_huffman_codes(root.right, prefix + "1", code_map)
return code_map5. Encode all characters to binary to compress
Once we have all the binary mappings for each character, We can encode characters from the original text to a new file with the binary codes for each character.
The code to do this is as simple as
def compress_text(code_map):
file = read('moby-dick.txt')
bitstring = ""
for c in file:
# this temp is just so all of it fits in one line
temp = code_map["<SPACE>" if c == " " else ("\\n" if c == "\n" else c)]
bitstring += temp
file.write('moby-dick-compressed.txt', bitstring)
6. Decode all characters back to original string
Before we call it a day, we need to decode the moby-dick-compressed.txt back to alphanumeric characters and make sure that the compression is lossless and accurate, to do this we traverse through the string and find the correct mapping for each character sequence by traversing the tree.
To be precise we traverse the string, for every character we move down on either the left or right subtree and continue till we hit a leaf node, once we hit a leaf node we know we have our next character.
The code for this would look along the lines of
def decode_huffman_compression(compressed_file, huffman_tree):
file = read(compressed_file)
decoded_chars = []
node = huffman_tree
for bit in file:
node = node.left if bit == "0" else node.right
if node.left is None and node.right is None:
c = node.char
if c == '<SPACE>':
c = " "
elif c == "\\n":
c = "\n"
decoded_chars.append(c)
node = huffman_tree
file2.create("moby-dick-reconstructed.txt")
file2.write("".join(decoded_chars))
Once reconstructed the file was identical to the original moby-dick.txt, i.e. the compression was lossless.
Wrapping up
Finally the size of the compressed binary file came out to be 5473 kB, which is a 43.7% reduction in size. Really loved reading up on these and implementing this on a book as large as Moby Dick. Was really really fun to use the data structures I've only seen on Leetcode in a more practical scenario.
pss pss you should soubscribe to my blog's mailing list. click here to do so.
PS click here if you wanna read other blogs I've written
Also if you wanna know more about Huffman Coding in the context of Information Theory, do check this out, was a very fun watch for me.
